Wanneer zijn twee driehoeken gelijkvormig?
Twee driehoeken zijn gelijkvormig als de driehoeken gelijk hebben:
- twee hoeken (hh)
- een hoek en de verhouding van de omliggende zijden (zhz)
- de verhouding van de zijden (zzz)
- een rechte hoek en de verhouding van twee niet-omliggende zijden (zzr)
Eén van de bovenstaande kenmerken is al voldoende om te stellen dat er sprake is van gelijkvormige driehoeken.
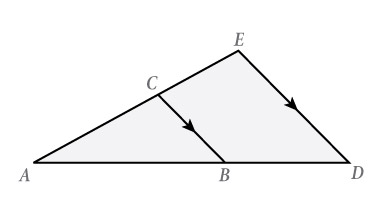 |
| ∠BAC = ∠DAE en ∠ACB = ∠AED (F-hoeken) ΔABC is dus gelijkvormig met ΔADE (hh) |
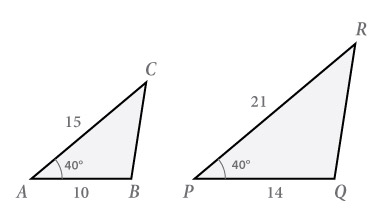 |
| ∠A = ∠P en AB : AC = PQ : PR ΔABC is dus gelijkvormig met ΔPQR (zhz) |
Gelijkvormige driehoeken kun je opvatten als driehoeken waarvan de ene driehoek een vergroting (of verkleining) is van de andere driehoek.
Basisvormen
Er zijn twee soorten gelijkvormige driehoeken die vaak voorkomen. Leer ze uit je hoofd zodat je ze snel in figuren kunt herkennen.
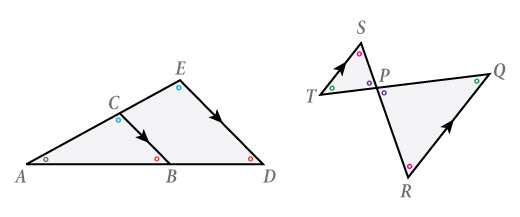 |
| Twee veelvoorkomende gelijkvormige driehoeken: de snavel (links) en de zandloper (rechts). Gelijke gekleurde cirkels geven gelijke hoeken aan. De pijlen geven evenwijdige lijnen aan. ΔABC is gelijkvormig met ΔADE. ΔPQR is gelijkvormig met ΔPTS. |