1. Home
  2. Scheikunde
  3. Redoxchemie
  4. Vraag

Hoe gebruik je de Wet van Nernst?

In Binas-tabel 48 of ScienceData-tabel 9.1f staat voor ieder redoxkoppel de standaardelektrodepotentiaal vermeld. Deze waarde is de standaardwaarde en geldt alleen als de concentraties van de opgeloste deeltjes in de halfreactie gelijk is aan 1,00 M. Op het moment dat de concentraties anders zijn, geldt een andere waarde voor de elektrodepotentiaal. Deze nieuwe waarde kan worden berekend met behulp van de wet van Nernst:

V = V0 + \( \mathsf { \large \frac{0,059}{n} \,}\)· log\( \mathsf { \large \frac{[ox]}{[red]} } \)

Hierin geldt dat:

  • V = de gemeten elektrodepotentiaal
  • V0 = de standaardelektrodepotentiaal
  • n = het aantal elektronen in de halfreactie
  • [ox] = de concentraties van de deeltjes aan de oxidatorkant van de halfreactie
  • [red] = de concentraties van de deeltjes aan de reductorkant van de halfreactie

Let op: de Wet van Nernst geldt alleen voor een halfreactie.
Let op: vaste stoffen en vloeistoffen worden niet vermeld in de Wet van Nernst.

Stel we hebben de volgende elektrochemische cel:

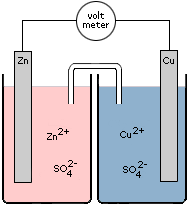
In de linker halfcel bevindt een Zn elektrode zich in een oplossing van zinksulfaat (0,1 M). Rechts bevindt zich een Cu elektrode in een oplossing van kopersulfaat (0,1 M). De deeltjes aan de linkerkant zijn Zn, Zn2+ en SO42−. De deeltjes aan de rechterkant zijn Cu, Cu2+ en SO42−.

De vraag is nu: wat reageert er als oxidator en wat reageert er als reductor? Volgens Binas-tabel 48 of ScienceData-tabel 9.1f is Zn de sterkste reductor (-0,76 V) en Cu2+ de sterkste oxidator (0,34 V).

De halfreacties die hier optreden zijn:

Zn(s)\(\rightleftarrows\)Zn2++2 e−voor de halfcel met de reductor

Cu2++2 e−\(\rightleftarrows\)Cu (s)voor de halfcel met de oxidator

Omdat de concentraties van de deeltjes in beide halfcellen niet gelijk is aan 1,00 M kunnen we niet gebruik maken van de standaardelektrodepotentiaal uit Binas-tabel 48 of ScienceData-tabel 9.1f. We zullen deze met behulp van de wet van Nernst zelf moeten bepalen. Voor de halfcel met de reductor geldt:

Vred = V0 + \( \mathsf { \large \frac{0,059}{2} \,}\)· log\( \mathsf { \large \frac{[Zn^{2+}]}{1} } \) = −0,76 + 0,0295 · log(0,1) = −0,79 V

Let op: de halfcel met de reductor bevat naast de reductor (Zn) ook zijn geconjugeerde oxidator (Zn2+). In de Wet van Nernst moet je deze twee concentraties invullen.

Let op: aangezien Zn vast is, kunnen we hiervoor geen concentratie invullen. De waarde van [red] in de bovenstaande wet van Nernst wordt dan ook 1.

Voor de halfcel met de oxidator geldt:

Vox = V0 + \( \mathsf { \large \frac{0,059}{2} \,}\)· log\( \mathsf { \large \frac{[Cu^{2+}]}{1} } \) = 0,34 + 0,0295 · log(0,1) = 0,31 V

De halfcel met de reductor heeft dus een potentiaal van −0,79 V. De halfcel met de oxidator heeft een potentiaal van +0,31 V.